Thermoset Cure Kinetics Part 7: TGA Kinetics

Guest Post by Dr. R. Bruce Prime

In the previous posts in this series we introduced basic principles of kinetics and the application of DSC to measure cure kinetics. Here we describe how thermogravimetric analysis or TGA can be applied to thermoset cure when the loss of mass is an integral part of the cure chemistry. The most common example is phenolics, where each bond formation is accompanied by the loss of a water and/or formaldehyde molecule, as illustrated here.

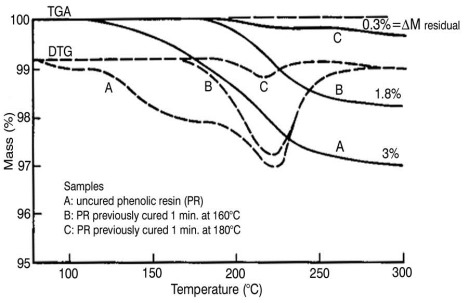
The figure below shows the TGA mass (m) and derivative DTG (dm/dt) curves for uncured and partially cured phenolic resin.

Phenolic cure. From From Cassel, PerkinElmer

Thermal Analysis Application Study (TAAS) 19 (1976).

Note the comparison to Isothermal Method 2 in Part 4 where samples were cured at various times and temperatures and then scanned in the DSC to measure residual cure. The DTG curve for the uncured resin shows three mass loss steps: one for loss of absorbed water (very small, only detected in DTG curve) and two associated with cure, ostensibly loss of water and formaldehyde. Assuming a one-to-one relationship between mass loss and conversion leads to the TGA analog of Eq. 9

For this system Dm_rxn = 3%. The sample cured 1 minute at 160°C shows a broad Dm_res of 1.8% that is predominantly the high temperature reaction, and translates to a = 0.40 º 40% cured. The sample cured 1 minute at 180°C shows a small mass loss (Dm_res = 0.3%) that is only the high temperature reaction and from Eq. 19 converts to 90% cure.

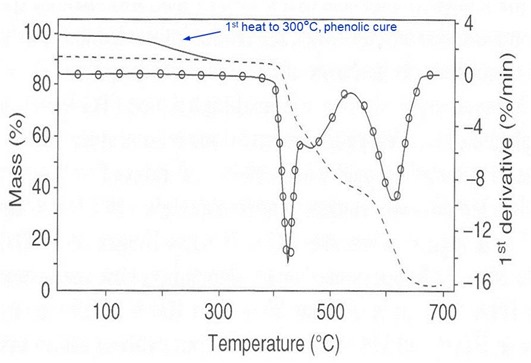
The material in the figure below is a thermoplastic-thermoset adhesive. The first heat shows ~10% mass loss attributed to the cure of the phenolic component.

TGA of thermoplastic-thermoset adhesive. From Tabaddor, Aloisio,

Bair, Plagianis and Taylor, J. Therm. Anal. Cal. 59, 559 (2000).

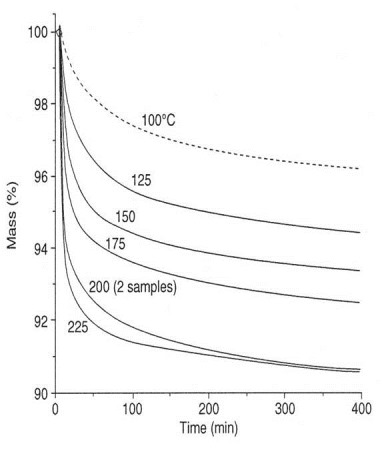
The figure below shows mass m vs. time for the phenolic at several isothermal cure temperatures. Note the comparison to Isothermal DSC Method 1.

By analogy with Eq. 7 in Part 4 the TGA conversion for this system is

where a_t,T is the conversion and Dm_t,T the mass loss at time t and temperature T.

As an example we calculate conversion at m_t,T = 96%, which occurs at all temperatures but different times in the figure above. Invoking Eq. 20 conversion is

In this manner conversion vs. time curves at all temperatures may be constructed, fit to different rate equations and analyzed for rate constants. Note however that T_g¥ for this phenolic is 235°C, which means that vitrification will occur at all temperatures, slow the reaction and complicate the kinetic analyses. The effects of vitrification are especially evident at lower cure temperatures. Note that vitrification will occur at higher conversion with increasing cure temperature.

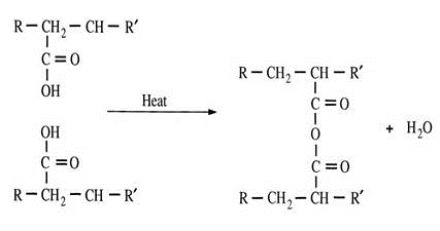
The example below shows the conversion of poly(acrylic acid) to the anhydride which eliminates one water molecule and creates one crosslink.

Scheme 4. Conversion of poly(acrylic acid) to anhydride.

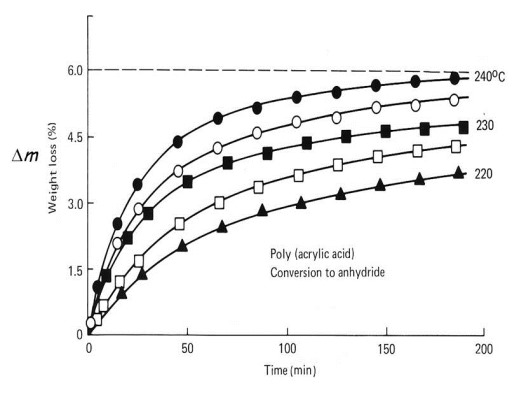
Isothermal TGA of Poly (acrylic acid). From Greenberg and Kamel,

J. Polym. Sci., Polym. Chem. Ed. 15, 2137 (1977).

The above figure shows mass loss Dm vs. time at five isothermal temperatures. For this study

From Scheme 4 we see that two acid moieties react to form one anhydride crosslink, suggesting the probability of 2^nd order kinetics, where

Since we are measuring a but not da/dt we need the integrated form of the 2^nd order equation

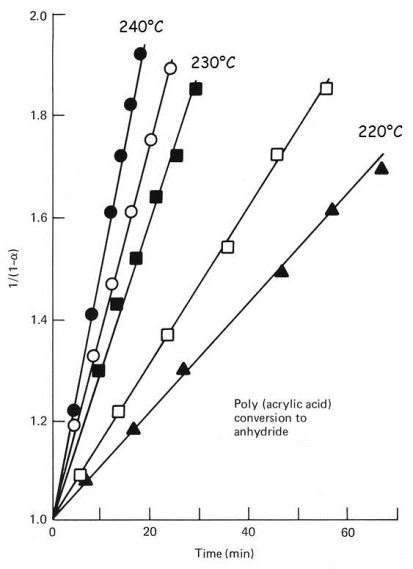
Thus if the cure reaction follows 2^nd order kinetics then a plot of 1/(1-a) vs. time will be linear with an intercept equal to one. The figure below verifies that this crosslinking reaction indeed follows 2^nd order kinetics. From Eq. 24 the slope is equal to the rate constant k and from the Arrhenius Eq. 2 a plot of ln k vs. T^-1 gives activation energy E and frequency factor A, at which point the kinetics for this system will be completely defined.

2^nd order plot for conversion of poly(acrylic acid) to anhydride. From From Greenberg and Kamel, J. Polym. Sci., Polym. Chem. Ed. 15, 2137 (1977).

 

To summarize, we have shown that TGA is as applicable as DSC to measure cure kinetics when there is a one-to-one relation between mass loss and crosslink formation. For such systems DSC will not be applicable because the endothermic mass loss will mask the cure exotherm.