Guest Post by Dr. R. Bruce Prime
 This is the first post in a new series on Thermoset Cure Kinetics, where we introduce the basic principles of kinetics and their general application to thermoset cure. In the following posts we describe important applications to the characterization and design of thermoset cure processes.
This is the first post in a new series on Thermoset Cure Kinetics, where we introduce the basic principles of kinetics and their general application to thermoset cure. In the following posts we describe important applications to the characterization and design of thermoset cure processes.
A common dictionary definition for kinetics is the branch of chemistry concerned with the rates of chemical reactions. In previous posts we have described some of the chemical reactions that form the basis for the cure of thermosets. For our purposes kinetics may be defined as mathematical relationships between time (t), temperature (T) and conversion (a). We consider two aspects of kinetics applied to the cure of thermosets.
The first is storage and work life kinetics after reactants have been mixed but prior to use. The objective in this case is to minimize the extent of reaction of a thermoset prior to its ultimate use. When reactants are mixed the cure reaction will begin immediately. The rate of reaction will depend on the reactivity of the reactants, the temperature and whether the system is liquid or solid. Means to extend the storage or work life thus include reducing the temperature, most effectively to 20 to 30°C below Tg so that the reactants are deep in the glassy state. Premixed and frozen adhesives are one example of a thermoset system that benefits from this approach. Prepregs, which are B-staged fiber reinforced composites, are another.
The second and more common use is the kinetics associated with completing the cure, e.g. in an adhesive joint or a fiber-reinforced composite. The objective here is to optimize the process in terms of physical properties, process time and energy consumed, which ultimately affect both the cost and the quality of the final part. Some cure processes are simple involving just a single time-at-temperature step. A simple exercise here could be calculation of the temperature increase necessary to reduce the cure time by 50%, a simple calculation if the activation energy is known. On the other end of the scale might be a composite cure process with two or more steps where resin viscosity needs to be controlled and pressure applied at just the right time. In this case the complete kinetic equations may need to be developed in order to model the cure process.
There are two principle equations associated with kinetics, referred to as the rate equation (Eq.1) and the Arrhenius equation (Eq. 2).
The terms in these equations are as follows
- a = conversion or degree of cure (unitless)
- da/dt = rate of conversion (sec-1)
- k = rate constant (sec-1)
- f(a) = kinetic model, explained below
- A = pre-exponential or frequency factor (sec-1)
- E = activation energy (kcal mol-1 or kJ mol-1), where J = joules
- R = gas constant (1.987 cal K-1 mol-1 or 8.314 J K-1 mol-1)
- T = absolute temperature in Kelvin (K)
In thermoset cure we consider two kinetic models, nth order and autocatalytic. The nth order equation is shown below (Eq. 3). An example is polyurethanes where an isocyanate reacts with an alcohol for form a urethane linkage (Scheme 1). Here a is the conversion of the reactants and (1-a) represents the concentration of reactants (isocyanate and alcohol) which varies from 1 at the start of the reaction to zero at the completion of the reaction. Because there are two reactants this is a second order reaction, i.e. the reaction order n = 2.
Scheme 1
A simple autocatalytic equation is shown in Eq.4. Note that a more detailed equation is often employed, as will be described in a later post.Here we consider the most common epoxy reaction of an epoxide with a diamine. Notice that this reaction produces an alcohol which is a catalyst for the epoxide-amine reaction, providing the autocatalytic nature of this cure chemistry. In Eq. 4 (1-a) represents the concentration of reactants (epoxide and amine) and a represents the concentration of alcohol produced in the reaction. In an ideal situation m=1 and n=2.
Scheme 2
In the next post we describe how one gets started with a kinetic study plus how to measure the activation energy for cure.
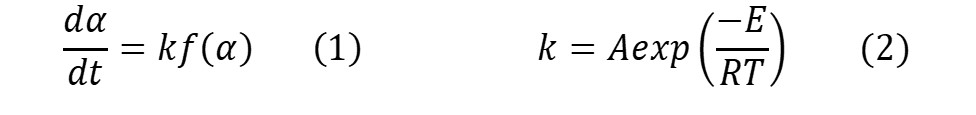
![clip_image002[6] clip_image002[6]](https://polymerinnovationblog.com/wp-content/uploads/2014/10/clip_image0026_thumb.png)
![clip_image002[8] clip_image002[8]](https://polymerinnovationblog.com/wp-content/uploads/2014/10/clip_image0028_thumb.png)
![clip_image002[10] clip_image002[10]](https://polymerinnovationblog.com/wp-content/uploads/2014/10/clip_image00210_thumb.png)
![clip_image002[12] clip_image002[12]](https://polymerinnovationblog.com/wp-content/uploads/2014/10/clip_image00212_thumb.png)
Nicely explained concept of curing kinetics of thermosets
Excellent blog, loads of really useful information. Please note there is a typo in equation 2, though it’s missing a negative sign!
Very well explained the cure kinetics of thermosets.
Hi,
thanks for the explanation.
I want to learn more about the equations. can I please get complete source of this information.
thanks you
great to read the post. its fruitful.