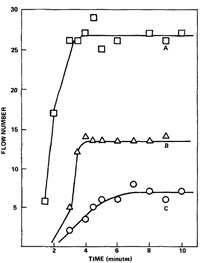
In the last post we presented the basics of the flow test and how to use the aborted flow test to determine the flow number as a function of time for various heating rates (figure on the left). In this post we will describe a method to measure flow continuously as a function of time. The focus here was to understand the large scale flow during lamination of large laminates and how the rheology impacts the flow. The flow test is a squeezing flow geometry.
The squeezing flow geometry was investigated in detail by several investigators including Leider (1), Leider and Bird (2) and Grimm (3) along with treatments by Bird, Armstrong and Hassager (4) and covered nicely by Macosko (5) There are multiple references in these two books to enable more in-depth study for the interested reader. Note that the original layup thickness is designated at 2h.
During lamination, the rate of plate motion is given by the Stefan equation (6):
Examination of the Stefan equation shows that the rate of plate motion (at constant force, F, and sample size R) is governed by two key parameters; the height of the layup and the viscosity. In theory, if one were to measure the plate motion as a function of time, one could develop a continuous measurement of the flow versus time during lamination.
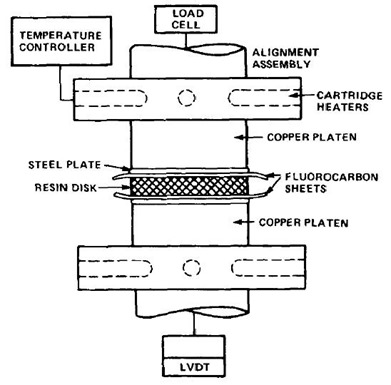
In the following figure, the experimental test figure used to precisely measure the plate closure is shown:
The above custom designed fixture was developed at Syracuse University under the direction of Dr. George Martin, Professor of Chemical Engineering and Materials Science and is described in Tungare, Martin, and Gotro (7). The fixture was used in a typical Instron test frame where the force could be carefully applied and measured by the load cell. The Instron frame had a linear variable differential transformer (LVDT) to measure the movement of the crossheads. In order to simulate the flow test conditions, a stainless steel plate, fluorocarbon release sheets and the prepreg layup could be loaded into the test frame. Note; a neat resin disk could also be pre-molded and used to investigate the viscosity profile for the resin only (7).
The conditions for the Stefan equation are:
- Plate separation changes sufficiently slowly (quasi-steady state)
- Stress overshoot and inertial terms are negligible
- Polymer may be approximates as Newtonian
At constant force, the Stefan equation may be integrated to obtain:
Note that the viscosity must be represented by an integral relationship due to the time-temperature dependence of the viscosity. Thus by measuring the plate closure rate insights into the viscosity profile could be obtained.
In the next post we will show how the time-dependent plate motion is related to the flow number and show experimental data of flow number versus time using the squeezing flow geometry.
References
1) Leider, Ind. Eng. Chem. Fundam., 13, 342 (1974)
2) Leider and Bird, Ind. Eng. Chem. Fundam., 13, 336 (1974)
3) Grimm, A.I.Ch.E. J., 24, 428 (1978)
4) Bird, Armstrong and Hassager (Dynamics of Polymeric Liquids, Vol 1. Fluid Mechanics, 2nd ed. Wiley, New York, p. 21, 1987
5) Macosko, Rheology Principles, Measurements, and Applications, VCH Publishers, p. 270, 1994).
6) Stefan, Sitzber. K. Akad. Wiss. Math. Natur., Wien, 69, Part 2, 713 (1874)
7) Tungare, Martin, and Gotro, Polym.Eng. and Sci., 28, no. 16, 1071, (1988)
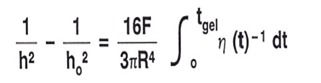
Leave a Reply