In previous posts, the characterization and rheological properties of highly filled systems was discussed. In particular, the rheological response of epoxies filled with the common thixotrope, fumed silica filler was covered in detail. Recall that the particle-particle interactions during shearing control to a large extend the viscosity shear rate relationship. When using fillers to modify both the rheological and final mechanical properties, there are other fillers to consider. Remember that the fumed silica is typically only added in small quantities. So what are some other common fillers and how do they impact both the rheology and the final properties of the cured formulation?
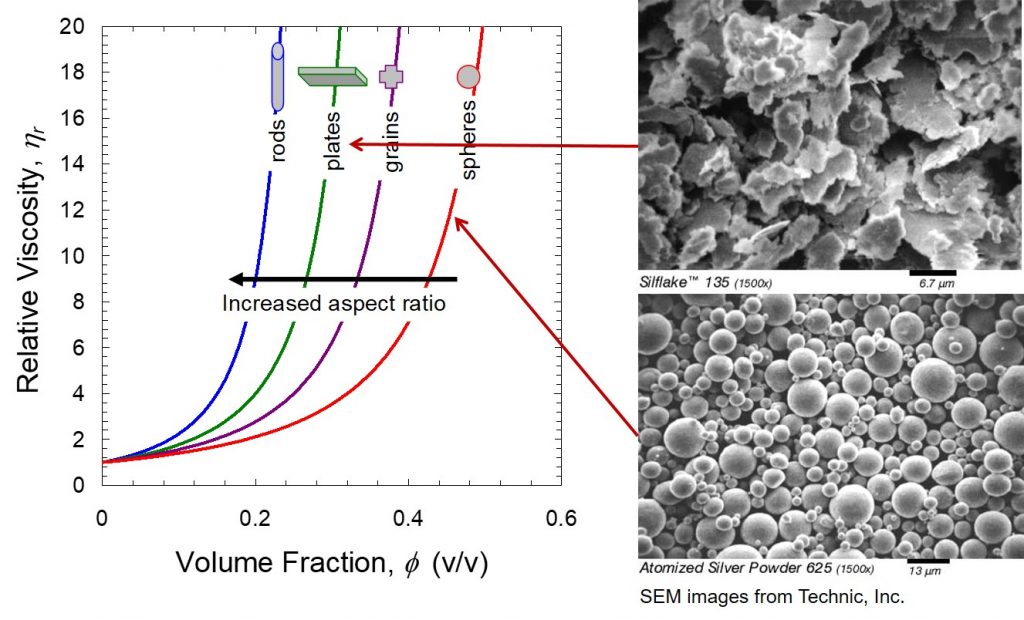
Figure 1. Viscosity as a function of aspect ratio and filler volume fraction. (Silflake 135 and Atomized silver power SEM images from Technic, Inc.)
The data in Figure 1 tells an interesting story. The relative viscosity is plotted so as to normalize all of the starting viscosities at 1 to enable clearly demonstrating the role of both filler loading (volume fraction) and filler aspect ratio. The most common filler is fused silica which would have the geometry of the silver powder in Figure 1. The spherical nature has the least impact on the viscosity. The silver or silica spheres can easily roll past one another during shearing. The loading level causes a sharp increase in the viscosity, even for the spherical particles. High filler loadings are required for many applications, such as to reduce the coefficient of thermal expansion, or to impart electrical or thermal conductivity.
For electrically conductive adhesives, silver flake is the preferred choice to get the maximum amount of particle-particle interactions (in this case flake-flake interactions). Think about silver flakes as poker chips. One can envision that it is much easier to get large interactions with poker chips compared to marbles. The large amount of interactions between flakes helps achieve the percolation threshold at lower filler loadings and facilitates electrical conductivity. However, the “poker chip” shape also causes a significant viscosity penalty as seen in Figure 1. Rod-like particles have the largest impact on the viscosity and this is potentially the reason nanotubes are typically only loaded in small percentages. Large amounts of rod-like fillers would severely limit the dispensing ability even at relatively low loadings.
A clever way to leverage the particle size dilemma is to use a hybrid filler geometry. Let’s say you need electrical conductivity, but need relatively high filler loading to achieve the desired conductivity but can’t really have a huge viscosity due to the dispensing constraints. One was around this is to use a combination of flake and powder as shown in Figure 2.
Figure 2. SEM image of Silflake 771 94-774 from Technic, Inc.
As clearly observed in Figure, the silver filler consists of a combination of flake and powders. Think of this as “raisin bran.” The silver flake will aid in getting good silver flake interactions and the silver powder will help lower the viscosity while also participate in the development of electrical conductivity. Depending on the ration of the flake to the powder, the viscosity curve will lie somewhere in-between the sphere and the plate curves in Figure 1. Working with your silver supplier, it might be possible to specify a given ratio of flake to powder to achieve the rheology and electrical performance required in your formulation. Other silver suppliers such as Metalor also provide “raisin bran” type silver fillers.
Particle size is another variable to consider as you are determining the role of fillers on the rheological properties.
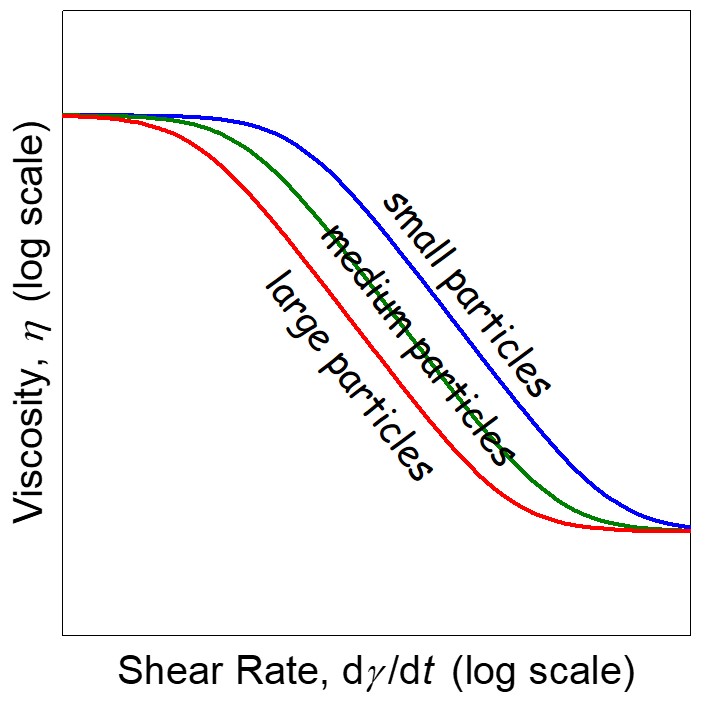
Figure 3. Schematic of the viscosity as a function of shear stress for three different particle sizes (at constant filler loading).
The particle size also has an impact of the viscosity profile. In the case in Figure 3, the dashed lines represent the yield points. The larger particles have a lower yield point while the smaller particles have a higher yield point. This seems backwards until you consider the surface area and as discussed earlier, the yield point is largely driven by a network structure resulting from particle-particle interactions. Smaller fillers have higher surface areas and thus potentially more particle-particle interactions. So we now see that the formulator and another “dial to turn” when developing highly filled materials.
Figure 4. Schematic of the viscosity as a function of shear stress for three different particle sizes (at constant filler loading).
As we have shown before, the viscosity shear rate, has a slightly different shape, but the impact of the particle size on the viscosity is the same, that is larger particles have a lower viscosity over a given shear rate range compared with smaller particles which have a higher viscosity as shown in Figure 4.
In summary:
- Filler aspect ratio plays an important role in controlling the viscosity shear rate relationship.
- The particle size is important in controlling the yield point
- The filler loading amount controls both the viscosity magnitude as well as the development of the yield point.
Carefully understanding the role of fillers and then using this understanding will allow the formulator to achieve both the desired rheological properties critical for dispensing, but also allow the final fully cured properties to be optimized. Fillers in action. Cool stuff!


Leave a Reply