Guest Post by Huan Lee, Lambient Technologies
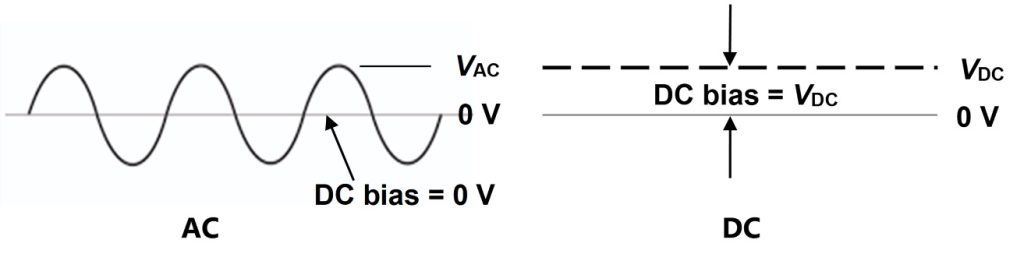
Both AC and DC measurements can probe the cure state of thermosets and composites, and it is important to understand their characteristics when deciding which to use. Dielectric cure monitoring, also called Dielectric Analysis (DEA) is an AC technique that excites a sensor with a sinusoidal signal of chosen frequency and amplitude, and a DC bias of zero volts. In contrast, DC resistance cure monitoring uses a constant bias voltage for the excitation. Figure 1 illustrates these two types of signals.
Figure 1. AC and DC excitations used for cure monitoring
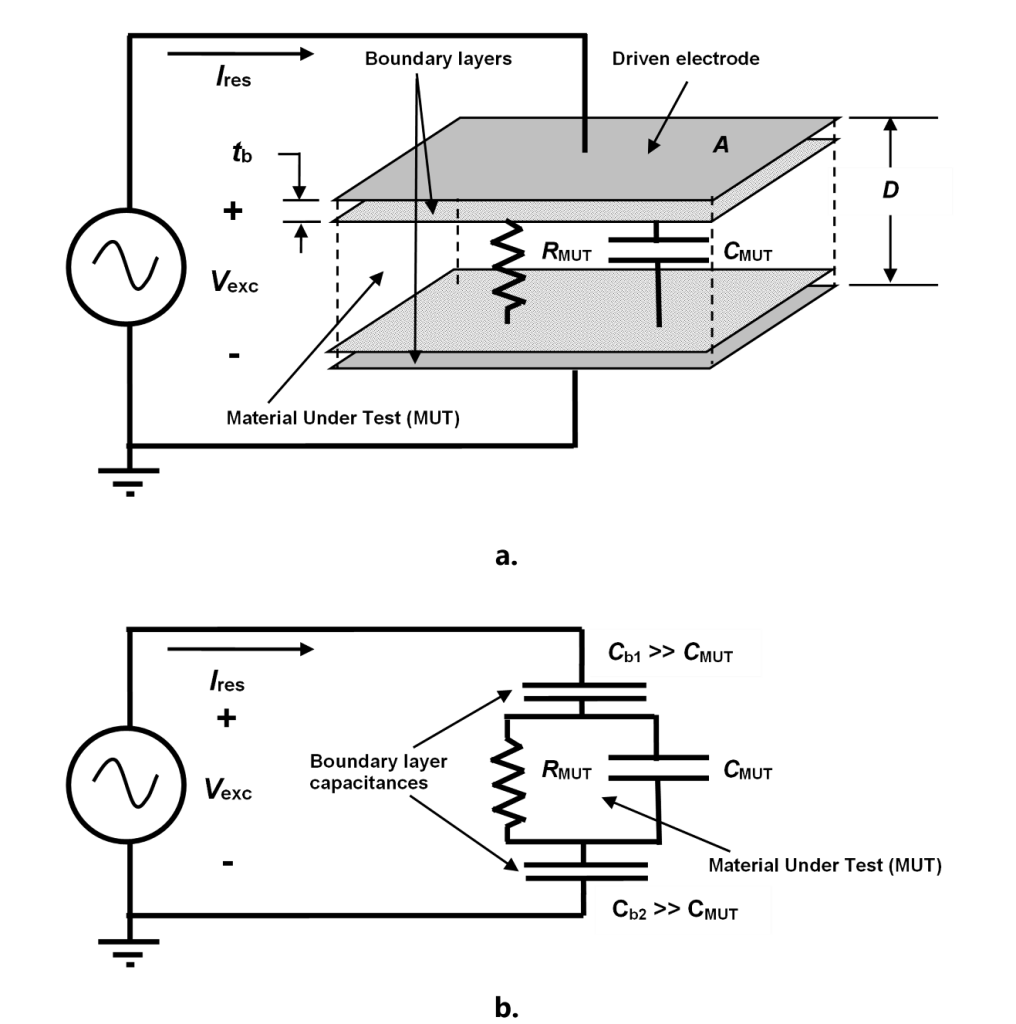
Figure 2.a. and Figure 2.b show the basic AC electrical model of a dielectric Material Under Test (MUT), consisting of a bulk resistance and capacitance, both in series with boundary layer capacitances caused by electrode polarization.
Figure 2. Physical (a.) and circuit (b.) models of thermoset resin for AC measurements
The material property of resistivity is calculated from the bulk resistance, scaled by a sensor’s cell constant. Although the DC resistivity (or resistance) of thermosets is commonly thought to be the same as frequency independent resistivity (or resistance), in fact they are different because resins can act as electrolytes instead of passive electronic components. Consequently, we should redefine these properties for materials subject to electrochemistry:
- DC resistivity (DC ion viscosity) – thermoset resistivity measured at f = 0 Hz with a DC bias
- Frequency independent resistivity (ion viscosity or AC ion viscosity) – thermoset resistivity that is constant or nearly constant across a range of AC frequencies and measured without a DC bias
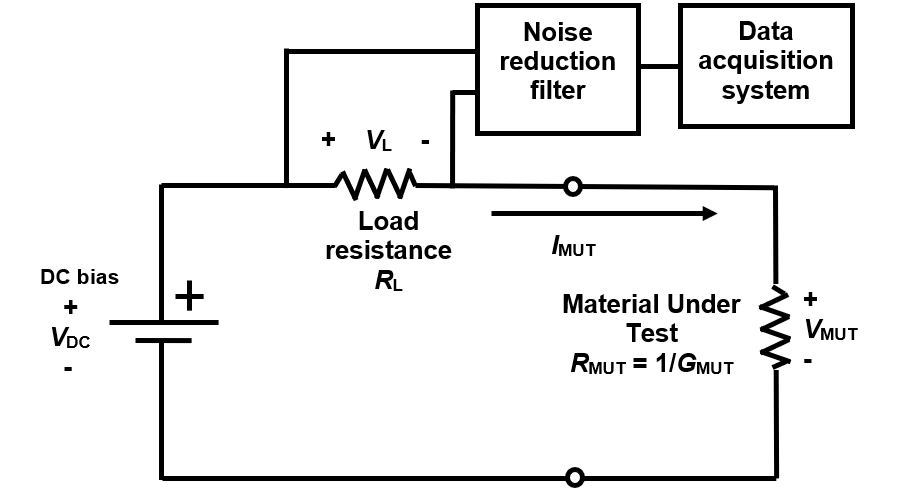
For studies of PR 520N [Ref. 1], an epoxy system formulated for resin transfer molding, we used the circuit of Figure 3 for DC cure monitoring, with load resistance RL determining the current through the sample. We made AC measurements with a “floating electrode” circuit [Ref. 2] widely used for dielectric cure monitoring.
Figure 3. Circuit for DC resistance cure monitoring
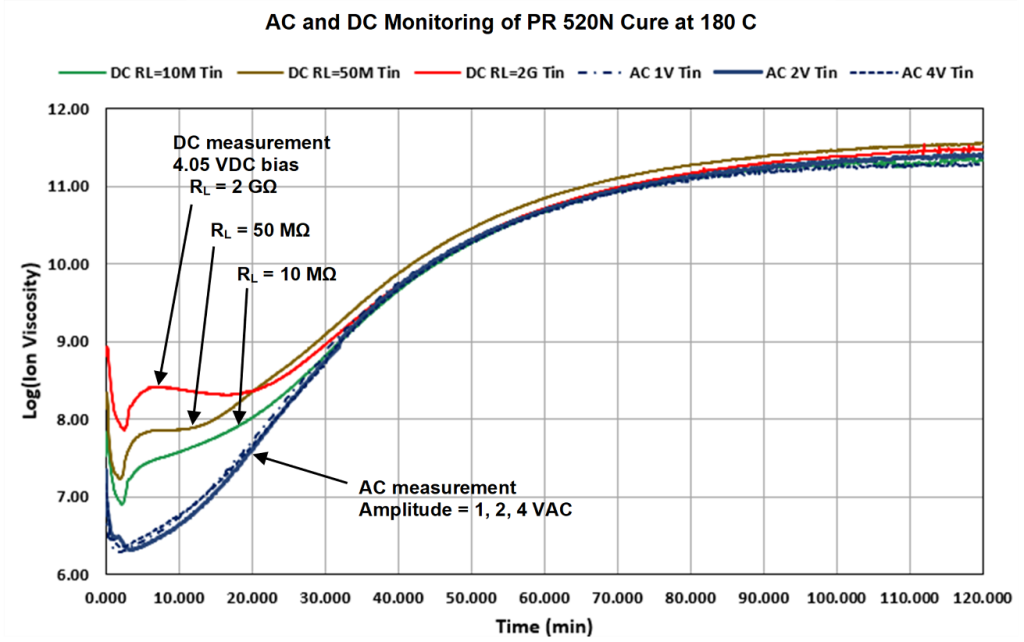
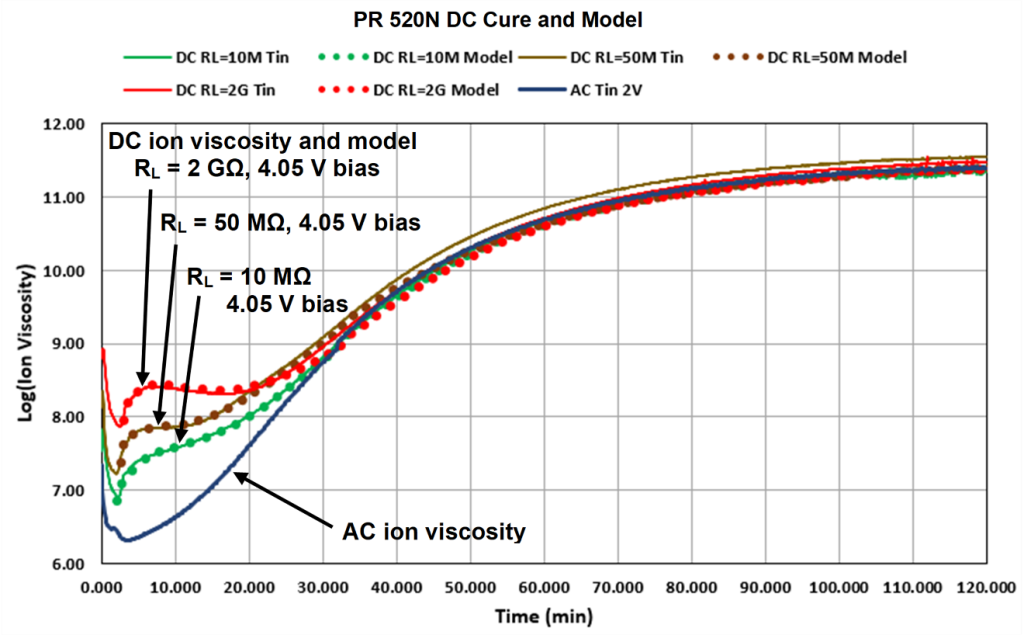
Figure 4 compares 10 Hz AC and DC data from PR 520N cured isothermally at 180 °C on Mini-Varicon sensors [Ref. 3]. As explained in the previous post, ion viscosity from a 10 Hz excitation accurately follows the entire cure. In subsequent tests, the ion viscosity curve did not change over a range of excitation voltages (1, 2 or 4 VAC), indicating AC ion viscosity is independent of the details of the measurement circuit.
DC ion viscosity, however, deviated significantly from AC results during early to mid-cure. Furthermore, DC ion viscosity varied with the load resistance (10 Mohm, 50 Mohm or 2 Gohm) and the resulting level of current.
Figure 4. 10 Hz AC and DC ion viscosity of PR 520N cure
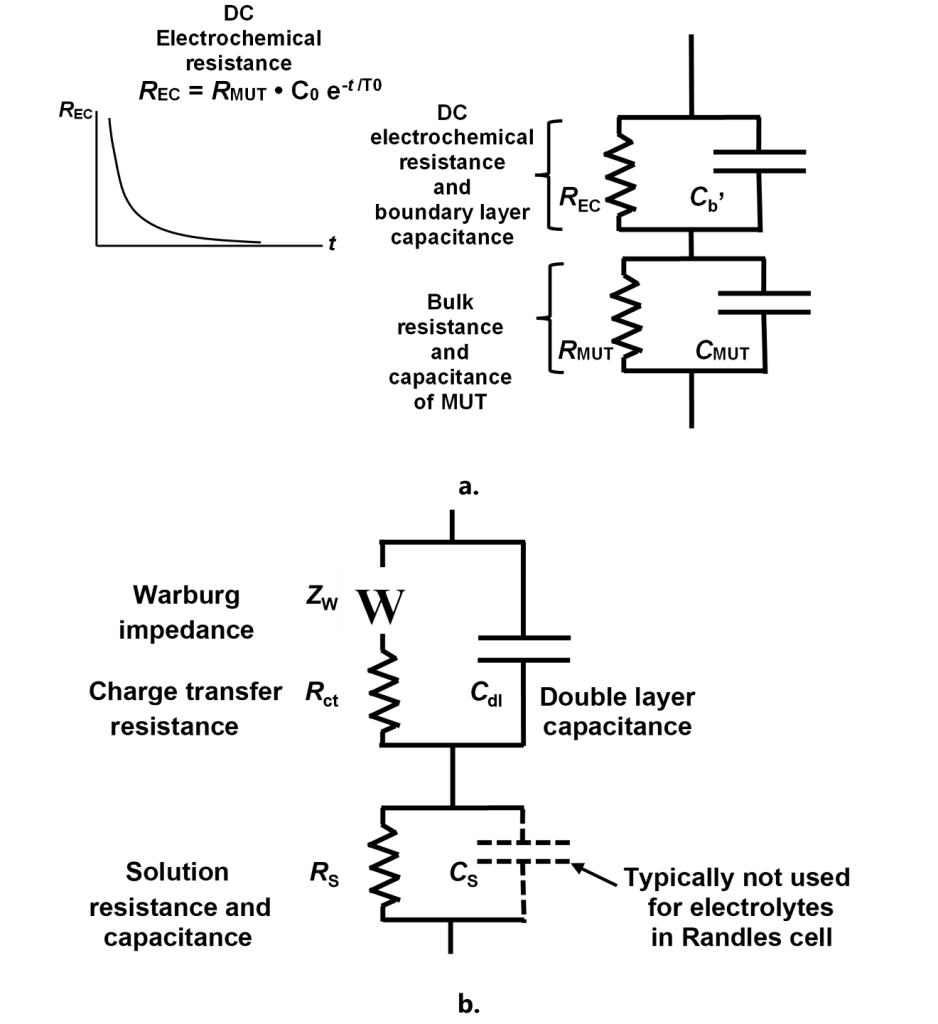
The discrepancies between AC and DC data can be modeled, as shown in Figure 5.a., with a DC electrochemical resistance in parallel with the boundary layer capacitance. Because the boundary layer capacitance shunts AC current around the DC electrochemical resistance, this additional resistance does not affect AC measurements.
The DC electrochemical resistance is proportional to monomer concentration and decreases exponentially with time as monomers are consumed in accordance with a first-order reaction. Consequently, DC measurements converge toward AC results at the end of cure, and also for highly resistive thermosets without significant electrochemistry.
Figure 5. Revised model of a thermoset resin (a.) and Randles cell (b.)
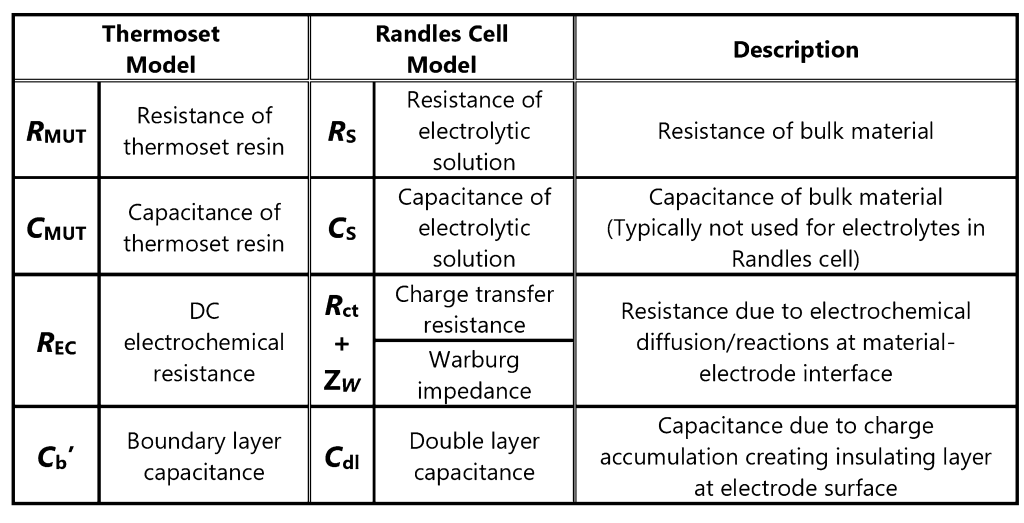
The revised thermoset model is analogous to the Randles cell of Figure 5.b., used in electrochemical impedance spectroscopy (EIS) for the study of electrolytes. During early cure, a resin may be treated as a highly resistive electrolyte and its boundary layer capacitance was long ago understood to be an electrolytic double layer capacitance. Similarly, the resin’s DC electrochemical resistance originates in reactions or ionic diffusion at the electrolyte-electrode interface. These resistances—the charge transfer resistance and the Warburg impedance—vary with applied voltage or current, as observed with the DC ion viscosity of PR 520N.
Table 1. Correspondence between thermoset and Randles cell models
For the DC ion viscosity of Figure 4, the humps between 5 and 15 minutes are a transient caused by current through the DC electrochemical resistance charging the bulk capacitance. By basic circuit theory, this transient response decays exponentially.
The revised thermoset model implies DC ion viscosity may be derived from AC ion viscosity by accounting for only two phenomena:
- A transient at the beginning of cure, and
- Consumption of monomers during cure
For the isothermal case, the following expression relates AC and DC ion viscosity by incorporating these two behaviors:
Figure 6 plots the model of Eq. 1 against actual PR 520N DC ion viscosity. For the first two minutes, DC ion viscosity decreased due to initial heating of the material, so data during this time was not included as cure. With proper selection of parameters, the revised thermoset model can reproduce DC ion viscosity from AC ion viscosity over the entire cure.
Figure 6. Model fit to DC cure data of PR 520N, 180 ºC isothermal cure
Knowing the differences between AC and DC measurements, we can now provide some guidance for their use:
- AC measurements at an optimum frequency can accurately follow the entire cure of most resins
- DC measurements have uncertain accuracy during early to mid-cure, and are most accurate during mid- to end of cure
- DC measurements can be useful for highly resistive materials like silicones, when AC measurements would require unfeasibly low frequencies and long measurement times
References
- Cycom PR 520N RTM manufactured by Solvay, Brussels, Belgium
- Application Note AN 3.25, “Dielectric Measurement Techniques,” Lambient Technologies, Cambridge, MA USA https://lambient.com
- Mini-Varicon sensor, manufactured by Lambient Technologies
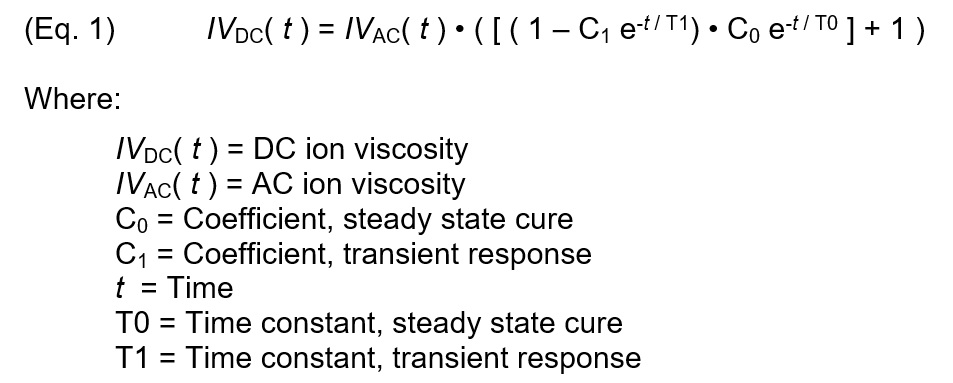

Hello
Thank you for such informative content.
I have one question related to Figure 4. We know that when the log ion viscosity reaches saturation or plateau then we say that the curing is completed. But as I can in this case, the plateau is not achieved, so how can we determine the end point of curing through this diagram?
Actually in my measurements sometimes I get this kind of issue too.
I would like to hear from you soon.
Thank you
Regards
Nitin gupta