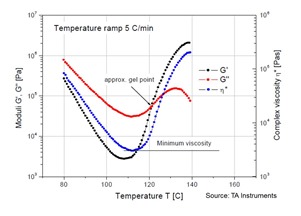
In previous posts we discussed how rheological techniques can be used to characterize the viscosity changes during thermoset curing. Dynamic parallel plates provide a means to measure the complex viscosity during either isothermal or non-isothermal cure profiles.
When I was at IBM my rheology work was focused on understanding the chemorheology during the lamination process for expensive multilayer circuit boards for mainframe computers. There were many layers of circuit cores with high performance thermoset prepregs in between. During lamination, the softening and flow (chemorheology) was a key process to ensure the circuit traces were completely encapsulated. If the flow wasn’t optimized then there could be voids which could lead to shorts and reliability issues. If the flow was too much or too little, the thickness between the layers would vary leading to inconsistent electrical signal integrity. If the viscosity of the softened prepreg was too high, then there would be inadequate wetting leading to potential adhesion issues. A lot was at stake.
An interesting challenge was to devise a way to measure the viscosity “in-situ” during the lamination process. As one might imagine, it was pretty difficult to embed a rheometer into the lamination press! One summer I was at a Thermoset Gordon conference and Prof. Stephen Senturia from MIT presented an interesting lecture on how they developed a small interdigitated comb electrode dielectric sensor. It was one of those “AHA!” moments. It turns out that they also formed a company called Micromet to commercialize the MIT technology. During one of the afternoon breaks, I met with Prof. Senturia and we hatched a plan to get one of his dielectrometers into my lab at IBM. We were off to the races!
So why did I think this would work? If you remember when we do dynamic mechanical measurements (either rheology or DMA) the sample is deformed using a sinusoidal deformation. If you remember, the equations for the DMA experiment are:
and from this relationship, the dynamic moduli can be calculated:
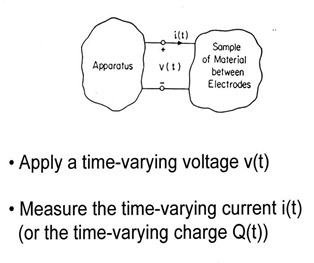
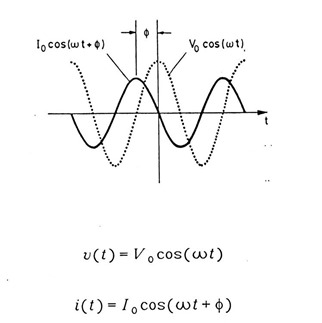
During the lecture, the thought that popped into my head was “is the polymer response to an applied sinusiodal voltage related to the response to the sinusoidal deformation in the dynamic mechanical experiment?” Let’s look at the equations for the dielectric experiment. In the following figure, we present a “black box” approach where we show the sample between two electrodes and the apparatus applies a time varying voltage and measures the time-varying current (or in the case of the microdielectrometer, the time-varying charge)
Now let’s look at the equations for the voltage:
This looks exactly like the dynamic mechanical analysis (in this case the cosine function is shown) but the features are the same. The resulting time-varying current has a phase lag just like the resulting stress in the DMA experiment. Analogous to the DMA equations, the dielectric permittivity and loss factor are calculated using the phase lag ( d )”:
In Part Two of this series we will discuss how dielectric measurements provide insight into the physics of the curing process.
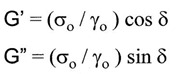
Leave a Reply